VIDEO

https://www.youtube.com/watch?v=7sv7UrLNecg&list=UUxwv8DxS24mOBZfa86w_wXQ

CONDICIÓN DE REFLEXIÓN TOTAL

  Reflexión total interna.

    Cuando la luz pasa de un medio óptimamente más denso, con índice de refracción  n₁, a otro medio óptimamente menos denso, con índice de refracción   n ₂ < n₁,  el ángulo de incidencia θ₁ será menor que el de refracción, θ₂  (fig.1a).  Por lo tanto, existe cierto ángulo de incidencia para el cual el ángulo refractado se hace igual a 90°, es decir, el rayo refractado se deslizara a lo largo de la superficie de separación de los medios sin entrar en el segundo medio (fig.1b).

                                       a)                                                      b)                                          c)  

                                                               

                                                                       Fig.1.

El ángulo incidente  para el cual el ángulo refractado es igual a 90° se denomina ángulo crítico (θ_c) o límite. Para todos los ángulos de incidencia θ₁ > θ_c no se produce rayo refractado: la luz se refleja por completo al primer medio. Este fenómeno recibe el nombre de reflexión total. El valor del ángulo crítico se determina, sustituyendo el ángulo refractado θ₂ por su valor de 90° en la fórmula que expresa la ley de Snell.

                                         

                                         

                                        

                                             

Esta igualdad se cumple solamente cuando n₁≥ n₂ , o en otras palabras, que la reflexión total puede producirse exclusivamente cuando la luz pasa de una sustancia de mayor densidad óptica a otra de menor densidad.

En la fig.1a  el ángulo de  incidencia  es menor que el ángulo crítico (θ₁< θ_c). En esta condición la intensidad del rayo reflejado es pequeña y la del refractado es mayor que la del reflejado. Cuando el ángulo de incidencia se aproxima al ángulo crítico el rayo refractado es casi rasante y de muy poca intensidad, mientras que el rayo reflejado aumenta su intensidad. Para los ángulos de incidencia que son mayores que el ángulo crítico (θ₁> θ_c), el rayo refractado desaparece (fig.1c) y tiene lugar la reflexión total, o sea, la luz se refleja totalmente.

TRANSFORMADORES DE CUARTO DE ONDA

Los transformadores son utilizados comúnmente para hacer acoples de impedancias y ésta no es la excepción. En el caso particular de las líneas de transmisión se acostumbra comúnmente el uso de transformadores de un cuarto de longitud de onda, el cual esta encargado de realizar procesos de compensación en las líneas de transmisión con cargas netamente resistivas y de valor diferente a la impedancia característica de la línea.

 

Figura 18. Transformador de un cuarto de longitud

Dependiendo del valor de la impedancia de carga, el transformador de un cuarto de longitud de onda puede comportarse como un transformador elevador o reductor cuando la impedancia de carga sea inferior o superior a la impedancia característica respectivamente. Este dispositivo no funciona dentro de un rango de frecuencias sino en una sola frecuencia. A continuación se explica el comportamiento del transformador de un cuarto de longitud de onda según el valor de la impedancia de carga.

R_L=Zo: El transformador se comporta como un transformador 1:1, quiere decir, que la señal de entrada es igual a la señal de salida

R_L>Zo: El transformador se comporta como reductor

R_L<Zo: El transformador se comporta como elevador

Un transformador de un cuarto de longitud de onda, en realidad no es un transformador sino una línea de transmisión que presenta un comportamiento semejante al de un transformador. Esta línea o transformador se conecta entre la línea de transmisión y la carga. La impedancia característica del transformador de un cuarto de longitud de onda se calcula de la siguiente forma:

ROE

La Razón o Relación de onda estacionaria o ROE es una medida de la energía enviada por el transmisor que es reflejada por el sistema de transmisión y vuelve al transmisor.

Teoría

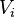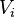En una línea de transmisión, coexisten una onda incidente, de amplitud , y otra reflejada, de amplitud .

Ambas ondas se combinan para dar una onda resultante.

La onda resultante puede tener dos valores extremos:

• Cuando la onda incidente y la onda reflejada produzcan una interferencia constructiva. En ese caso  y por lo tanto, la amplitud de la onda resultante es máxima
• Cuando la onda incidente y la onda reflejada se anulan recíprocamente (interferencia destructiva). En ese caso, .

El ROE (SWR en inglés, ROS en francés) se define como la relación entre ambos valores extremos

Los teóricos definen el coeficiente de reflexión Γ como la relación entre ambas amplitudes, reflejada sobre incidente:

Para tener en cuenta la diferencia de fase entre ambas ondas, es preciso escribir Γ como un número complejo. Por esa razón, Γ sigue las reglas especiales de la matemática compleja. Sin embargo, en la práctica, para simplificar se utiliza ρ, el módulo del número complejo Γ :

El valor de ρ puede expresarse como un porcentaje; en ese caso, se lo llama ROE (Razón de ondas estacionarias).

En ese caso, escribiremos  y  en función de ρ :

• ;
• .

Eso permite deducir una nueva expresión del ROE, esta vez en función de ρ :

COEFICIENTE DE REFLEXIÓN Y TRANSMISION

El coeficiente de reflexión es utilizado en física y en Ingeniería cuando se consideran medios con discontinuidades en propagación de ondas. Un coeficiente de reflexión describe la amplitud (o la intensidad) de una onda reflejada respecto a la onda incidente. El coeficiente de reflexión está estrechamente relacionado con el coeficiente de transmisión.

Distintos campos de la ciencia tienen diferentes aplicaciones para este término.

Una parte de la onda se transfiere y otra se refleja cuando pasa de un medio a otro. El coeficiente de reflexión determina la relación entre las ondas incidente y reflejada.

El coeficiente de transmisión se utiliza en física y en Ingeniería cuando se consideran medios con discontinuidades en propagación de ondas. El coeficiente de transmisión describe la amplitud (o la intensidad) de una onda transmitida respecto a la onda incidente. El coeficiente de transmisión está estrechamente relacionado con el coeficiente de reflexión.

Distintos campos de la ciencia tienen diferentes aplicaciones para este término.

INCIDENCIA NORMAL

LOS DOS LADOS DEL ESPEJO La cantidad de luz reflejada o transmitida por una superficie cualquiera (como la de un vidrio o la que separa el agua del aire) depende mucho del ángulo con el que llegua la luz a la superficie. Si llega rasante se refleja un porcentaje muy elevado de la luz (hasta el 100 %) mientras que si incide perpendicularmente (se dice incidencia normal) la cantidad de luz reflejada es muy poca (del orden de 5% en vidrio o en agua). A la luz transmitida le pasa todo lo contrario por conservación de la energía: muy baja transmisión en incidencia rasante y muy alta en incidencia normal.

                          

Una buena ilustración de este efecto se muestra en la imagen siguiente tomada en las tablas de Daimiel. En la parte inferior de la imagen se puede apreciar por transmisión el fondo rojizo de la laguna. La incidencia es casi normal y por lo tanto la proporción de luz transmitida es mayor que la reflejada. Por contra, hacia la parte superior de la imagen aumenta el ángulo de incidencia de la luz y por lo tanto empieza a ser mayor la cantidad de luz reflejada que la transmitida y cada vez se ve más nítidamente reflejado el cielo y la vegetación. De paso puede apreciarse que la imagen reflejada del cielo es más blanca (menos azul) cuanto más cerca del horizonte.

                         

                                          

REFLEXIÓN DE ONDAS PLANAS EN UNA INTERFAZ MATERIAL

Reflexión La reflexión de una onda es el rebote que experimenta cuando llega a un obstáculo grande, como una pared. Aunque el obstáculo absorba parte de la energía recibida (incluso vibrando si entra en resonancia) se produce también reflexión en la que se transmite de vuelta parte de la energía a las partículas del medio incidente. En la figura adjunta se representa un frente de ondas plano llegando a una superficie horizontal con un cierto ángulo i de incidencia (se mide con respecto a la dirección normal, N) De acuerdo con el principio de Huygens, cuando el frente de ondas empieza a "tocar" la superficie, el punto A se convierte en un nuevo foco que emite ondas secundarias y según transcurre el tiempo y el frente AB va incidiendo, repiten este comportamiento todos los puntos de la superficie comprendidos entre A y C. El frente de ondas reflejado, DC, es el envolvente de las ondas secundarias que se han ido emitiendo durante un tiempo igual al periodo desde el tramo AC de la pared. Aplicando leyes de geometría elemental al proceso, se llega a la conclusión de que el ángulo de incidencia i es igual al ángulo de reflexión r (ley de la reflexión) Puedes consultar la deducción de esta ley en el documento vinculado. Refracción La refracción de una onda consiste en el cambio de dirección que experimenta cuando pasa de un medio a otro distinto. Este cambio de dirección se produce como consecuencia de la diferente velocidad de propagación que tiene la onda en ambos medios. En la figura adjunta se representa la refracción de una onda plana desde un medio 1 a otro medio 2, suponiendo que la velocidad de propagación es menor en el segundo medio que en el primero. A medida que el frente de ondas AB va incidiendo en la superficie de separación, los puntos AC de esa superficie se convierten en focos secundarios y transmiten la vibración hacia el segundo medio. Debido a que la velocidad en el segundo medio es menor, la envolvente de las ondas secundarias transmitidas conforma un frente de ondas EC, en el que el punto E está más próximo a la superficie de separación que el B. En consecuencia, al pasar al segundo medio los rayos se desvían acercándose a la dirección normal N. Mediante un razonamiento similar se comprueba que la desviación de la dirección de propagación tiene lugar en sentido contrario cuando la onda viaja de un medio donde su velocidad de propagación es menor a otro en el que es mayor. Para describir formalmente la refracción de ondas luminosas (no mecánicas) se define el índice de refracción de un medio, n, indicando el número de veces que la velocidad de la luz es mayor en el vacío que en ese medio. Es decir, el índice de refracción es igual a 1 en el vacío (donde la luz tiene su máxima velocidad, 300000 Km/s) y mayor que la unidad en cualquier otro medio. En el documento vinculado se deduce la ley de la refracción, expresada en función del índice de refracción (ley de Snell). Normalmente la reflexión y la refracción se producen de forma simultánea. Cuando incide una onda sobre la superficie de separación entre dos medios, los puntos de esa superficie actúan como focos secundarios, que transmite la vibración en todas las direcciones y forman frentes de onda reflejados y refractados. La energía y la intensidad de la onda incidente se reparte entre ambos procesos (reflexión y refracción) en una determinada proporción. El dibujo animado adjunto muestra el rayo luminoso reflejado y el rayo luminoso refractado cuando incide luz procedente de un medio material (n=1.5) hacia el vacío (n=1.0) Obsérvese que a partir de un cierto valor del ángulo de incidencia no se produce refracción y toda la energía de la onda se traslada al frente de ondas reflejado. Este fenómeno se llama reflexión total y se explica teniendo en cuenta que, en este caso, el ángulo de incidencia es menor que ángulo el de refracción. Al aumentar el primero lo hace también el segundo hasta el límite de 90º, por encima del cuál evidentemente no se produce la refracción.

ONDAS ESTACIONARIAS

PROPIEDADES DE LAS ONDAS - Ondas estacionarias Las ondas estacionarias son ondas producidas en un medio limitado, como, por ejemplo, una cuerda elástica no muy larga y fija en al menos uno de sus dos extremos. Para generar en dicha cuerda una onda estacionaria, se puede atar por un extremo a una pared y hacer vibrar al otro con una pequeña amplitud. Se obtienen pulsos transversales que viajan hasta la pared, donde se reflejan y vuelven. La cuerda es recorrida por dos ondas de sentido opuesto y se producen interferencias que, en principio, dan lugar a unas oscilaciones bastante desordenadas. Aumentando la frecuencia con la que se agita el extremo de la cuerda se puede conseguir que las oscilaciones adquieran el perfil mostrado por la figura adjunta. Corresponde a una onda en la que aumenta sensiblemente la amplitud y tiene un vientre fijo en el centro y dos nodos también fijos en los extremos. Esta onda se llama estacionaria porque, a diferencia del resto de ondas, en las que se aprecia un avance de las crestas y los valles, no parece moverse. Si se fijan los dos extremos de la cuerda y se estira transversalmente de uno, dos, tres puntos se puede generar en la cuerda una secuencia de ondas estacionarias con un número creciente de nodos y vientres, como las indicadas en la figura adjunta. Una propiedad destacada de estas ondas estacionarias es que su longitud de onda (y, consecuentemente, su frecuencia) no puede adoptar cualquier valor arbitrario, sino sólo unos determinados valores que se relacionan con la longitud de la cuerda, mediante las siguientes expresiones: l1 = 2L,   l2 = 2L/2,   l3 = 2L/3,   l4 = 2L/4,...   ln = 2nL/4   (siendo n = 1, 2, 3,..) Teniendo en cuenta que c = l/T  = ln,  las frecuencias correspondientes son: n1 = c/2L    n2 = 2c/2L    n3 = 3c/2L    n4 = 4c/2L,..    nn = nc/2L   (siendo n = 1, 2, 3,..)